About 9 months ago I wrote a post about graphics programming for 6502 based computers, if you haven't read it I encourage you do so to have the context for understanding this post. I decided to come back to this, and do some more with it. This is my follow up post, things are not perfect, and I've still got improvements to make.
When I was writing my original post, I plotted the coordinates by hand on a 320x200 plane. While this works for static graphics, it does not work when you need to dynamically update the screen.
I was drawing shapes at set coordinates, and their position on the plane was hardcoded. What if I want to update their positions or scaling? This is where I came up with a new approach.
For line shapes, I created an array of lines. These lines start at (0,0) which in this instance is the top left of the screen.
/* Array of a shape to be drawn
* {x1, y1, x2, y2}
* {x1, y1, x2, y2}
* {x1, y1, x2, y2}
* ...
*/
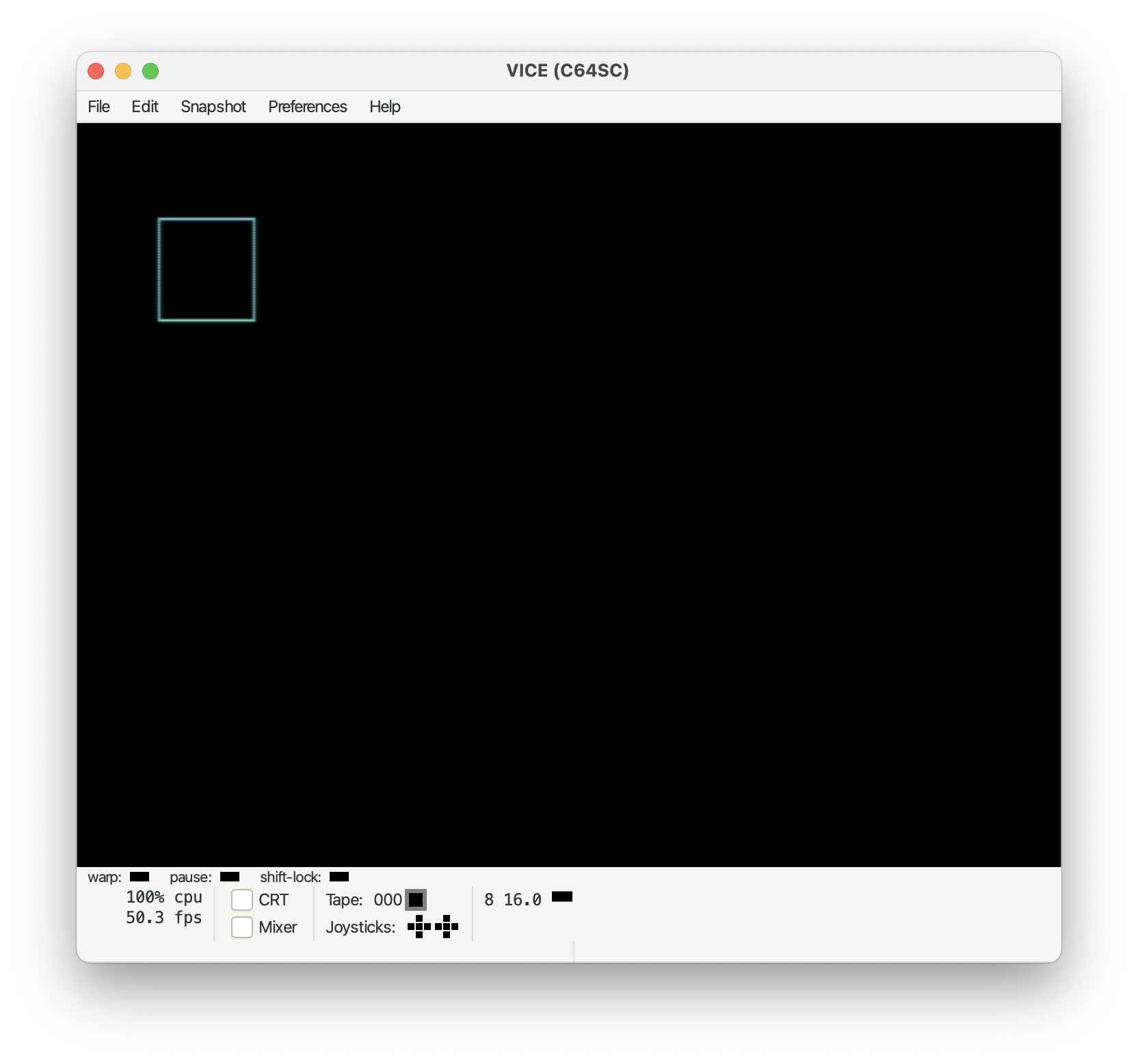
The base coordinates of a 37x37 square are:
const unsigned int square[4][4] = {
{0, 0, 0, 37},
{0, 0, 37, 0},
{37, 0, 37, 37},
{37, 37, 0, 37}
};
The tgi_line() function begins drawing at (0,0) and keeps going to (0,37). Then it begins drawing at (0,0) and stops at (37,0). Then it begins drawing at (37,0) and stops at (37,37). Lastly it begins drawing at (37,37) and stops at (0, 37).

The way to position objects on the screen is by adding an x and/or y offset to the base coordinates.
I will show a visualization using a program called Pixen available on macOS. Using this program, I can draw on a 320x200 space representative of the Commodore 64 display, and the bottom tells me which coordinates a pixel is on. This is great for prototyping what you want to draw on the screen.
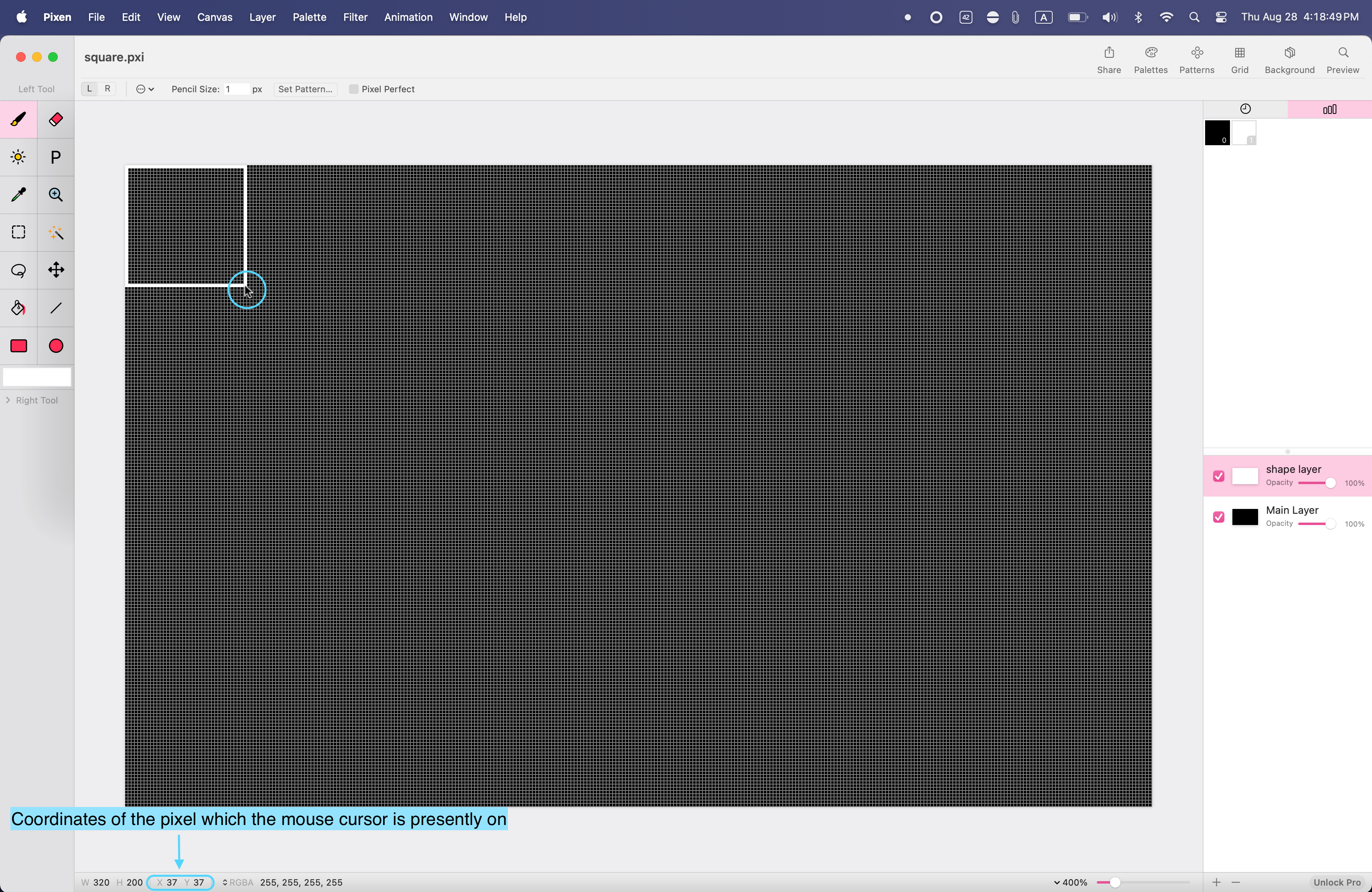
How would we draw this in code? We can create a loop like such which plots the pixel pairs on the screen and loops through the 2d array:
int i;
int x = 0;
int y = 0;
for (i = 0; i < 4; i++)
tgi_line((square[i][0]) + x, (square[i][1]) + y, (square[i][2]) + x, (square[i][3]) + y);
This will draw the square at (0, 0) which is the top left corner of the screen in this case.
I created draw functions for doing this:
/* Take the x and y coordinates where you to begin drawing your shapes on the screen, add those to the line coordinates of the shape.
* Take in a scale factor, multiple the shape coordinates by it. For example, to upscale the square by 2 multiply by 2
*/
void draw_square(const unsigned int x, const unsigned int y, unsigned int scale) {
unsigned int i;
for (i = 0; i < 4; i++)
tgi_line((square[i][0] * scale) + x, (square[i][1] * scale) + y, (square[i][2] * scale) + x, (square[i][3] * scale) + y);
}
I decided to go ahead and draw a neocat using this method, first I draw the neocat in pixen. I included the file here.
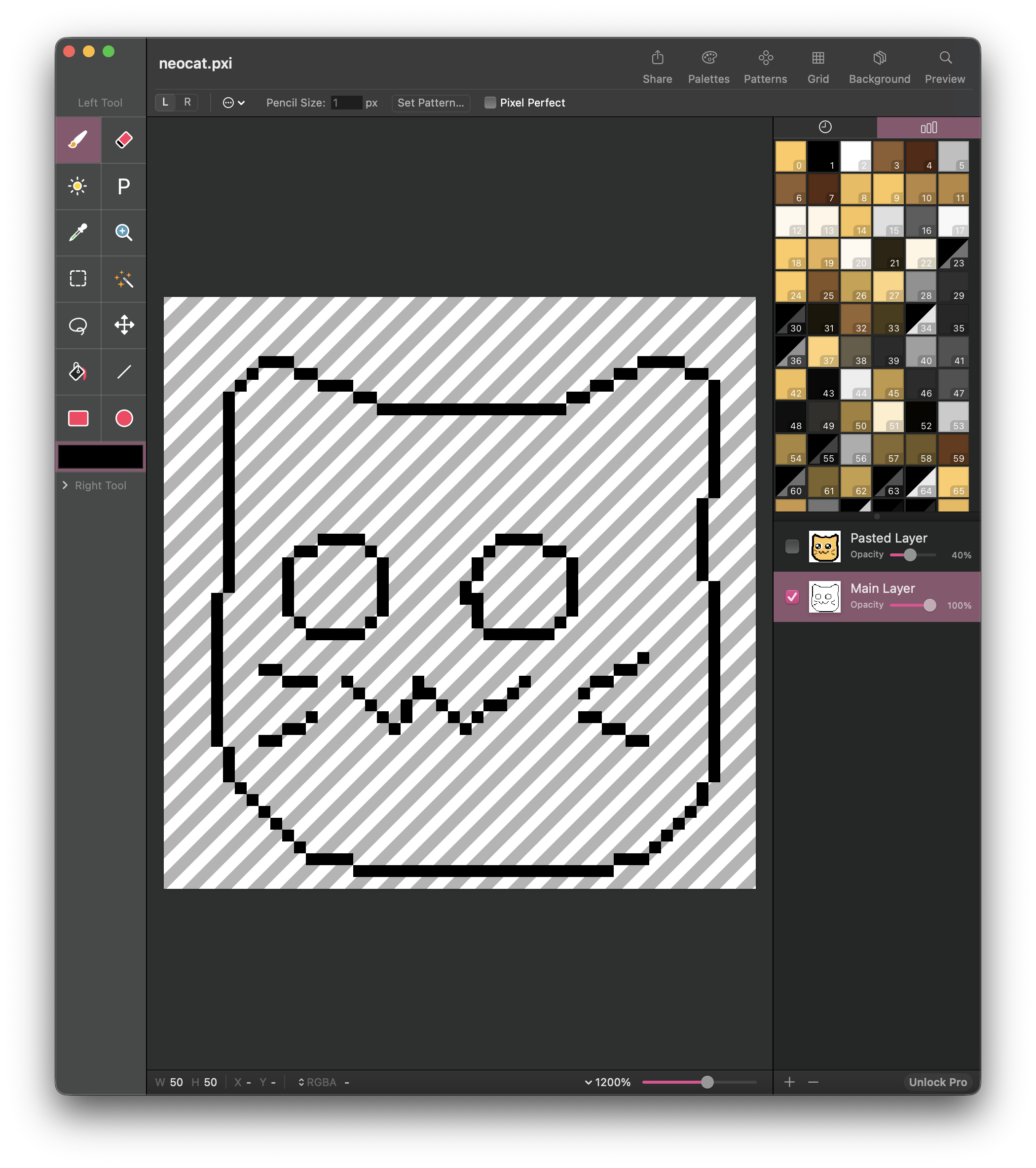
Next I used my mouse cursor to hover over and record the coordinates, and created a 2d array in my C program with the coordinates:
const unsigned int neocat[51][4] = {
// Outline
{8, 5, 5, 8},
{5, 9, 5, 24},
{4, 25, 4, 37},
{5, 38, 5, 40},
{6, 41, 11, 46},
{12, 47, 15, 47},
{16, 48, 37, 48},
{38, 47, 40, 47},
{41, 46, 44, 43},
{45, 42, 45, 41},
{46, 40, 46, 24},
{45, 23, 45, 17},
{46, 16, 46, 7},
{45, 6, 44, 6},
{43, 5, 40, 5},
{40, 5, 33, 9},
{33, 9, 18, 9},
{18, 9, 15, 7},
{15, 7, 13, 7},
{13, 7, 10, 5},
{10, 5, 8, 5},
// Eyes
{13, 20, 10, 22},
{10, 22, 10, 26},
{10, 26, 12, 28},
{10, 5, 8, 5},
{12, 28, 16, 28},
{16, 28, 18, 26},
{18, 26, 18, 22},
{18, 22, 16, 20},
{16, 20, 13, 20},
{28, 20, 26, 22},
{26, 22, 26, 23},
{26, 23, 25, 24},
{25, 24, 25, 25},
{26, 25, 26, 27},
{27, 28, 32, 28},
{32, 28, 34, 26},
{34, 26, 34, 22},
{34, 22, 31, 20},
{31, 20, 28, 20},
// Whiskers
{8, 31, 9, 31},
{10, 32, 12, 32},
{12, 35, 8, 37},
{40, 30, 35, 33},
{35, 35, 40, 37},
// Mouth
{15, 32, 19, 36},
{19, 36, 21, 32},
{22, 32, 25, 36},
{25, 36, 30, 32}
};
Finally I wrote a function for drawing it:
void draw_neocat(const unsigned int x, const unsigned int y, unsigned int scale) {
unsigned int i;
for (i = 0; i < 51; i++)
tgi_line((neocat[i][0] * scale) + x, (neocat[i][1] * scale) + y, (neocat[i][2] * scale) + x, (neocat[i][3] * scale) + y);
}
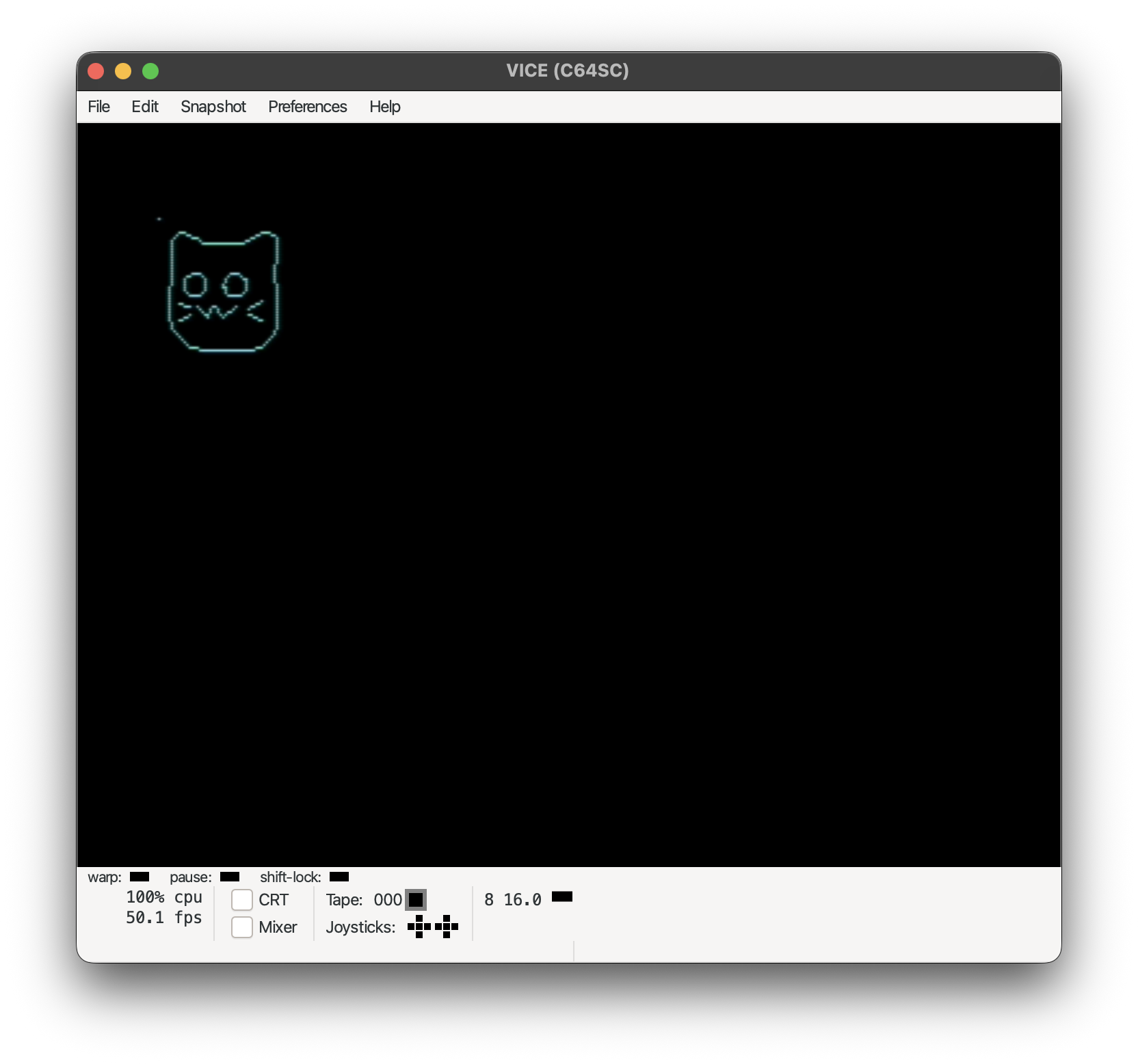
I've noticed that the more complex the shape is, the more error prone it is to upscale. For instance, you can see with the neocat that when upscaling it, not all the lines appear connected anymore.
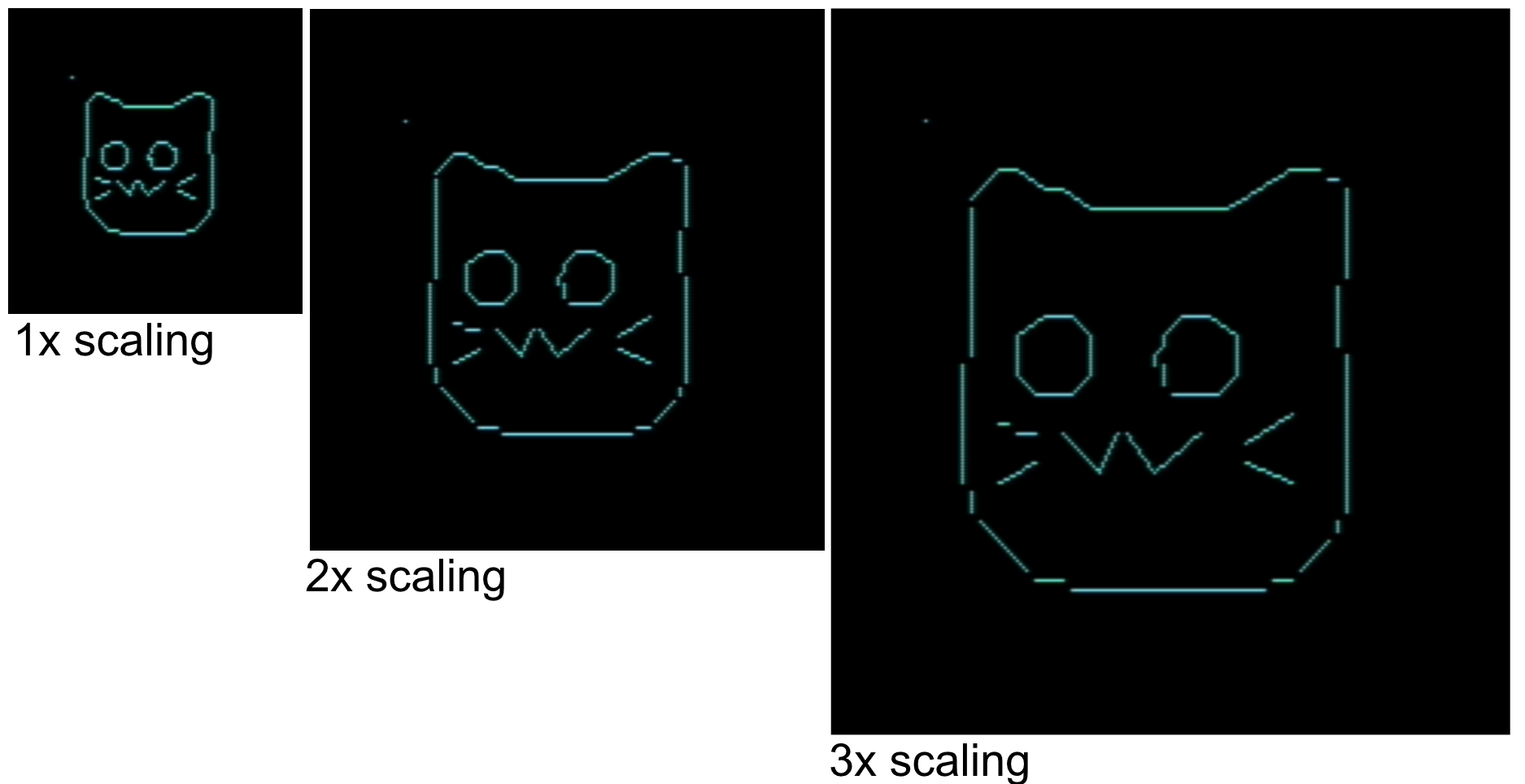
Additionally, the more complex a shape is the harder it is to draw. This becomes apparent if you want to do any sort of animation, where it has to redraw graphics again and again.
You can move the graphics by adding and subtracting the offset you want to move from the base coordinates.
An example of this is moving a square around using the wasd keys:
while (running) {
input = cgetc();
switch (input) {
// WASD move the square around
case 'w': {
tgi_clear();
y -= 10;
draw_square(x, y, scale_factor);
break;
}
case 'a': {
x -= 10;
tgi_clear();
draw_square(x, y, scale_factor);
break;
}
case 'd': {
x += 10;
tgi_clear();
draw_square(x, y, scale_factor);
break;
}
case 's': {
y += 10;
tgi_clear();
draw_square(x, y, scale_factor);
break;
}
}
}
This is an example of an animation of a square moving around on the screen:
while (playing) {
for (x = 0, y = 0; x < 320 && y < 200; x++, y++) {
draw_square(x, y, 2);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (y = 200; y > 0; y--) {
draw_square(x, y, 2);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 200, y = 0; x > 0 && y < 200; x--, y++) {
draw_square(x, y, 2);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 0, y = 200; x < 320 && y > 0; x++, y--) {
draw_square(x, y, 2);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 320; x > 0; x--) {
draw_square(x, y, 2);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
}
More complex animations are harder on the CPU to draw, so they end up being much worse performing.
Here's an example of a neocat animation:
while (playing) {
for (x = 0, y = 0; x < 320 && y < 200; x++, y++) {
draw_neocat(x, y, scale_factor);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (y = 200; y > 0; y--) {
draw_neocat(x, y, scale_factor);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 320, y = 0; x > 0 && y < 200; x--, y++) {
draw_neocat(x, y, scale_factor);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 0, y = 200; x < 320 && y > 0; x++, y--) {
draw_neocat(x, y, scale_factor);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
for (x = 320; x > 0; x--) {
draw_neocat(x, y, scale_factor);
tgi_clear();
if (kbhit()) {
goto clr;
}
}
}
Up to this point I've been using TGI's line drawing functions to draw shapes and graphics, however TGI has built in shape drawing functions. This includes functions for drawing shapes like rectangles, elipses, and circles.
These functions are:
tgi_arc(int x, int y, unsigned char rx, unsigned char ry, unsigned sa, unsigned ea); // Draws an elliptical arc, the center is at the x and y coordinates, and the rx and ry coordinates are the radii, the sa and ea are start and end angles
tgi_bar(int x1, int y1, int x2, int y2); // Draws a bar (rectangle) at these set coordinate pairs
tgi_circle(int x, int y, unsigned char radius); // Draws a circle with the center at the x and y position of a given radius
tgi_ellipse(int x, int y, unsigned char rx, unsigned char ry); // Draws an ellipse, the center is at the x and y coordinates, and the rx and ry coordinates are the radii
tgi_pieslice(int x, int y, unsigned char rx, unsigned char ry, unsigned sa, unsigned ea); // Draws a pie slice, the center is at the x and y coordinates,the rx and ry coordinates are the radii, and the sa an ea are the start and end angles
The bar drawing function is the only one which fills in the shape, the others draw an outline but don't fill it in. Here's some screenshots below of each function in use.
Arc:
tgi_arc(160, 100, 80, 40, 0, 180);
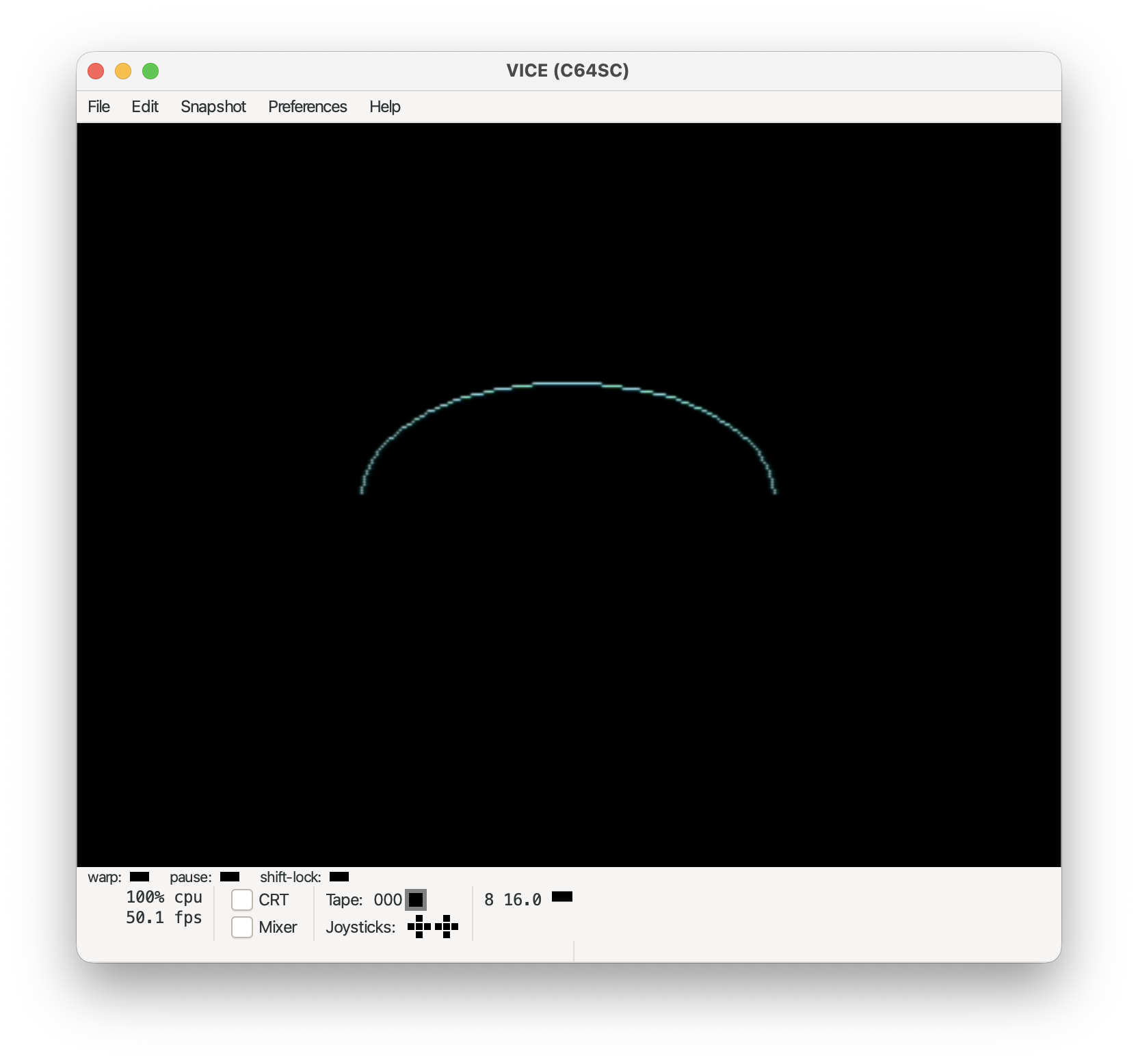
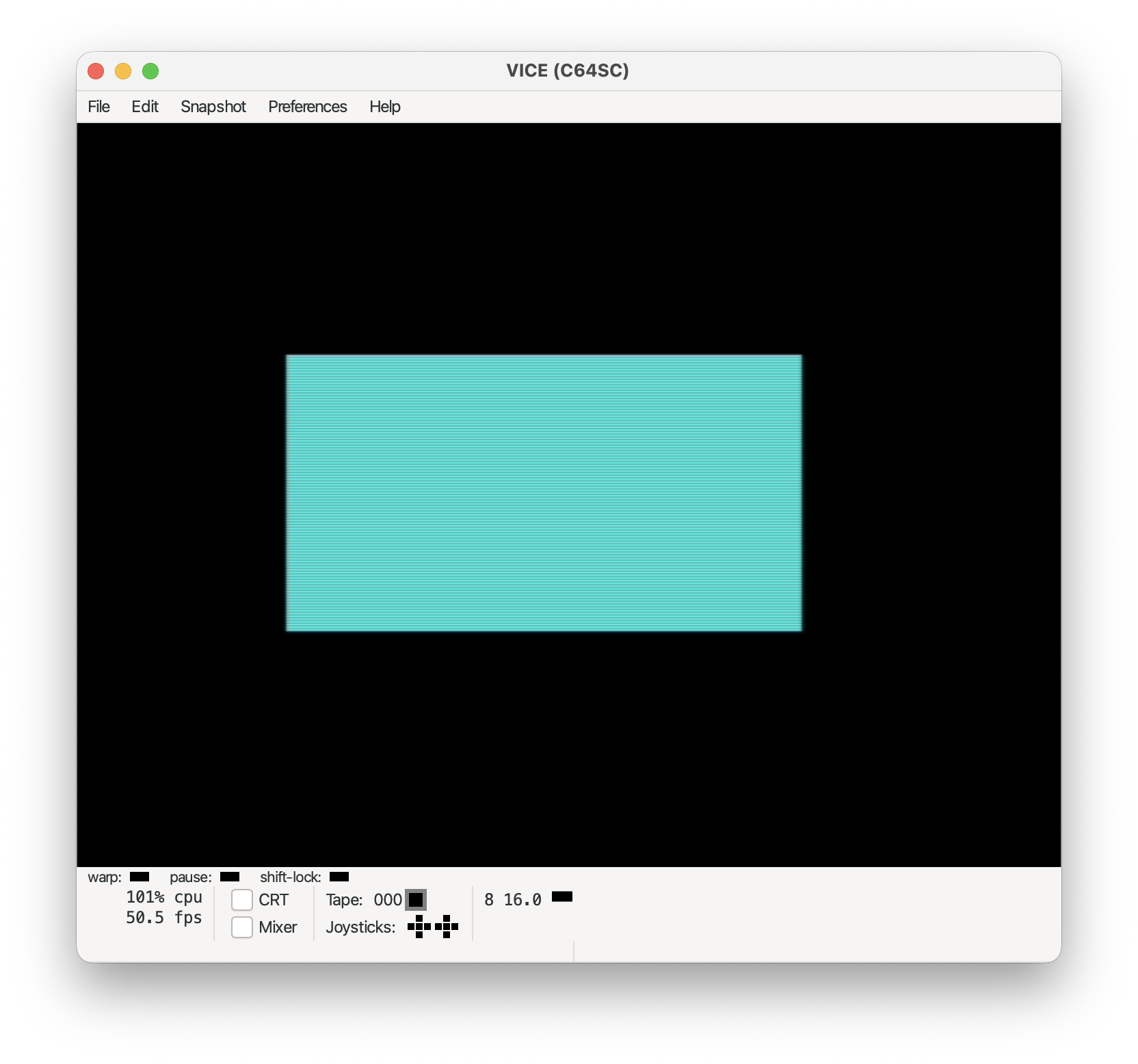
Bar:
tgi_bar(50, 50, 250, 150);
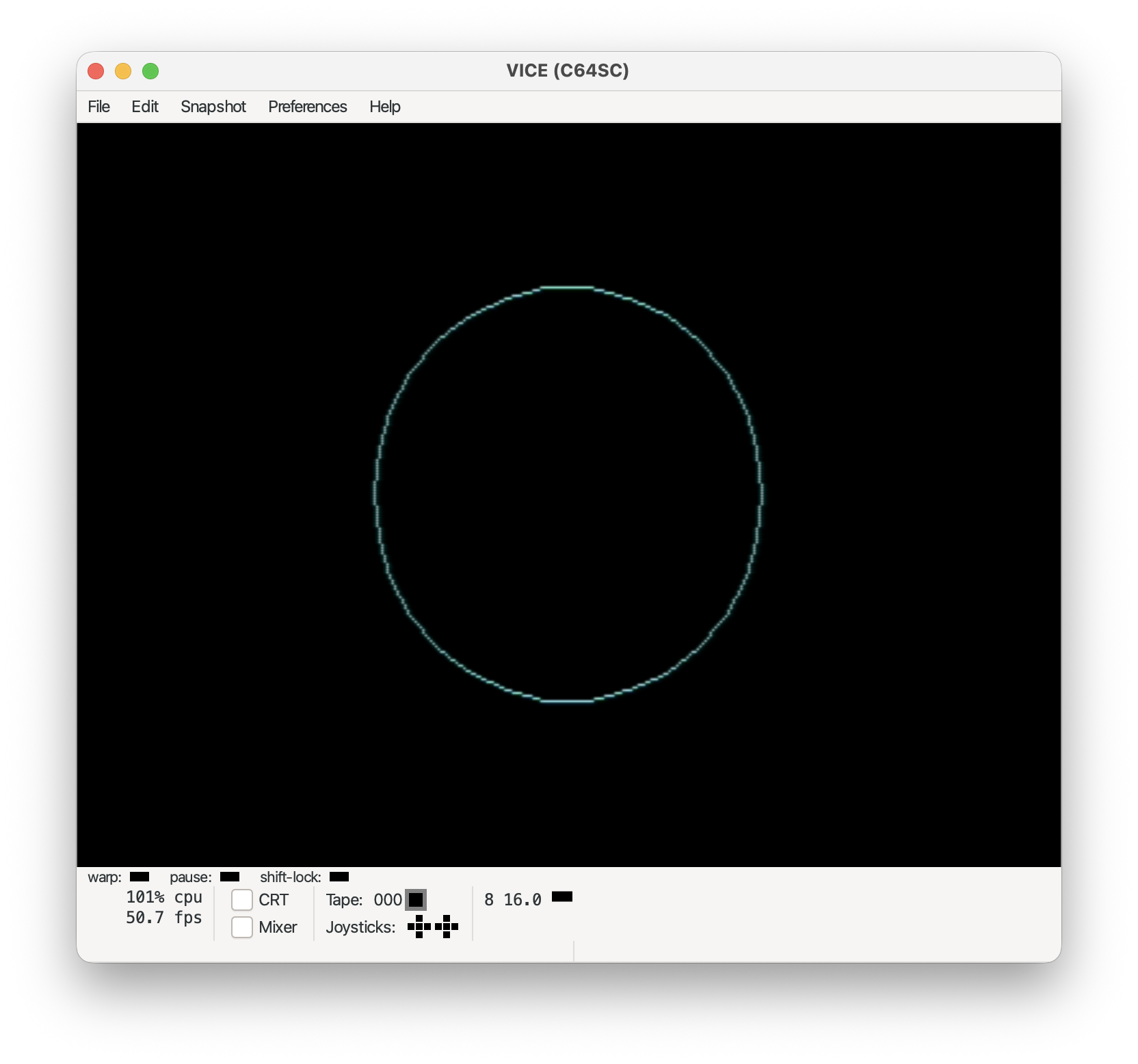
Circle:
tgi_circle(160, 100, 75);
Ellipse:
tgi_ellipse(160, 100, 80, 40);
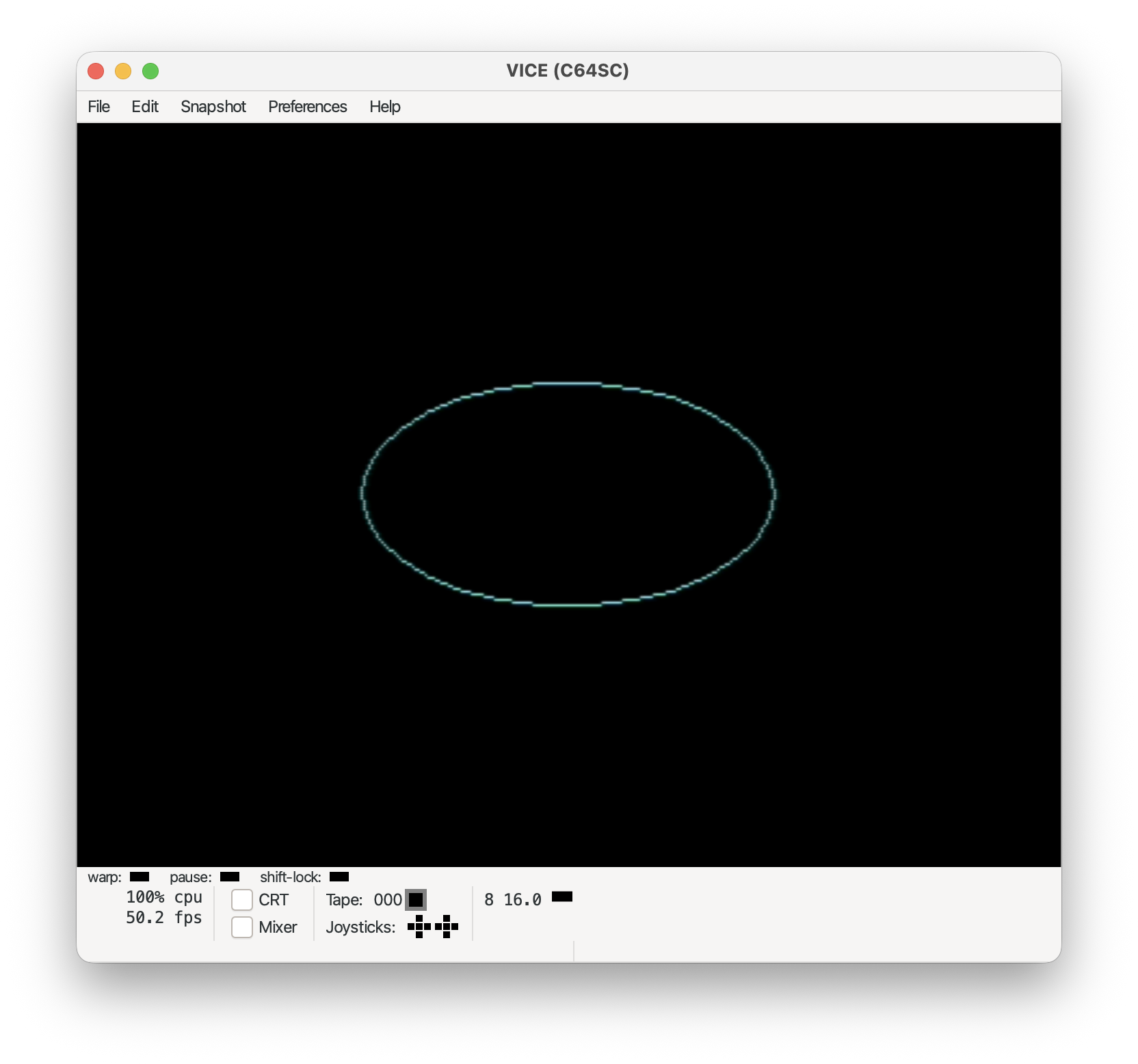
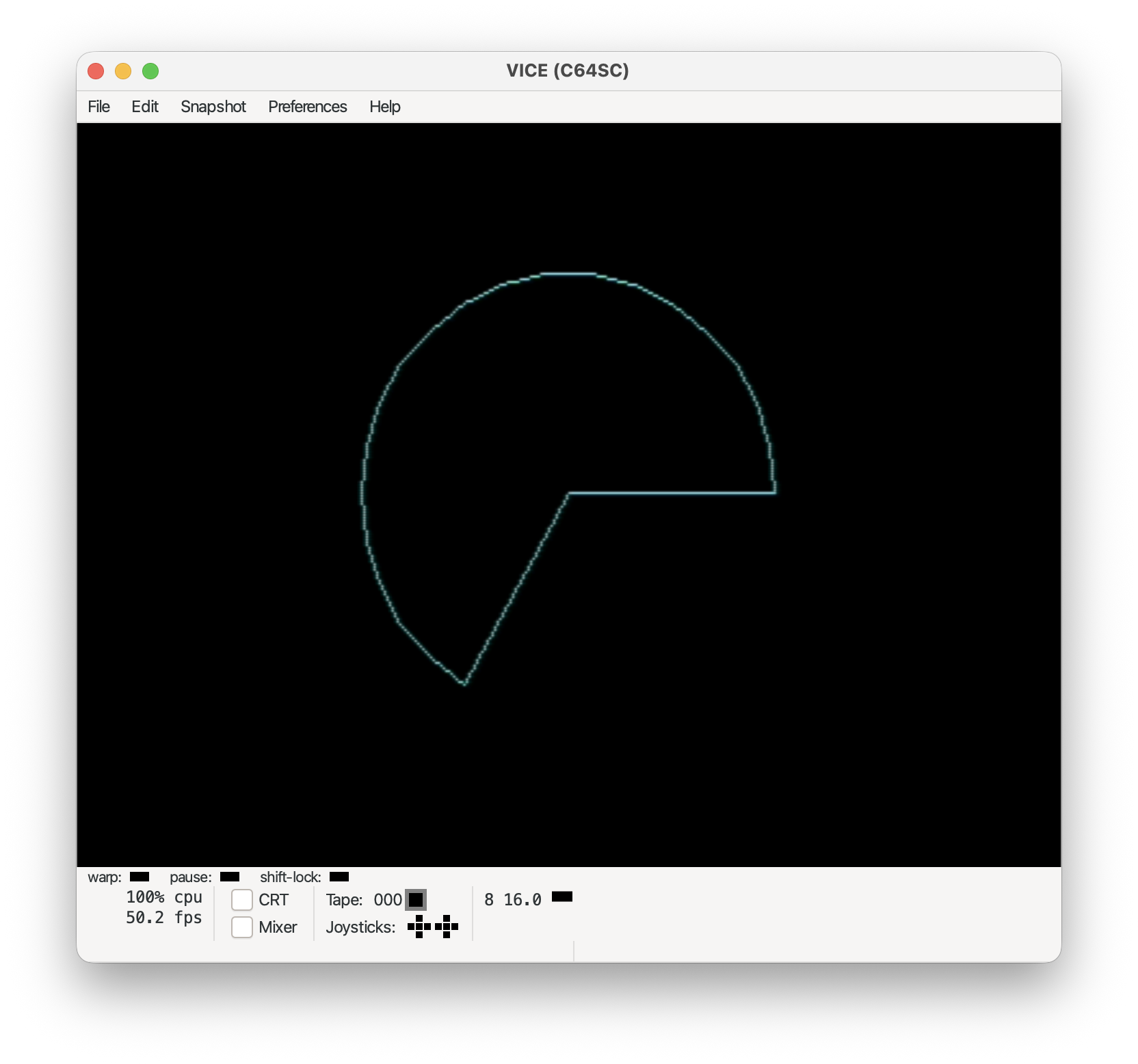
Pieslice:
tgi_pieslice(160, 100, 80, 80, 0, 240);
In conclusion, the TGI library makes graphics programming for 6502 based 8-bit computers very doable, but it has performance issues from drawing and redrawing graphics on the screen. However, if you're looking to get started I think it's a good option and I learned a lot from it.